You are here: Panda Wiki>EMC Web>ForwardEndcapMeetings>Minutes2015-01-19 (2015-01-23, FritzHerbertHeinsius)Edit Attach
Minutes of the forward endcap EMC meeting, 19th of January 2015, SeeVogh, 14:00-15:45
Topics are not in the order of discussion, but by subject. Presence- Basel: Werner, Irakli, Natalie
- Bochum: Cathrina, Claudius, Fritz-Herbert, Malte, Mario, Matthias, Patrick, Stephan, Tobias H., Tobias T., Tom
- Bonn: Christoph
- Groningen: Myroslav
- Uppsala: Pawel
- GSI: excused
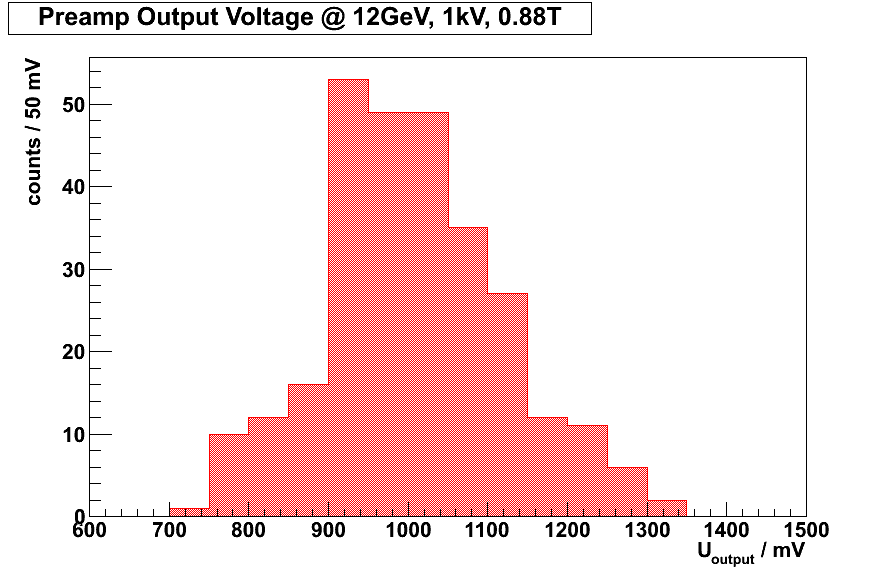
- Measurements of VPTTs show that preamplifiers with 3 different gains are needed. See attached plot from Tobias H. (For 0.5V/pC standard preamp). For final definition we will wait for all VPTTs (beginning of March)
- Gain will be optimized for 2.2 V maximum amplitude
- Werner: Production of preamps takes 3-4 month.
- Basel will start with production of "medium" gain preamps, once gain is defined
- APD preamp: no news from Bochum concerning test of ringing for special APD preamp with increased gain compared to preamps with reduced gain (Action: Bochum)
- Matthias tested shaper based on KVI design, as currently implemented in the ADC.
- Shaper not optimized for Basel preamp. Single ended 50 Ohm termination required. Implementation of splitting high/low gain while keeping 50 Ohm termination unclear.
- Need to maximize the signal, filter parameters not optimized for rise time. (Discussion: cut off needed for pileup events, but may be optimized)
- Suggestion to design two different boards, one optimized for endcap and Basel preamp (single ended 50 Ohm dual gain and shaping), one optimized for ASIC (differential, single gain, no shaping) and required barrel form factor.
- There is some DC coupling, which causes an amplitude dependance on the baseline (some %)
- Action Myroslav: Check effect of base line shifts on amplitude.
- Action Pawel: Optimize shaper/filter for 2.2 V input with Basel preamplifier (Note from Matthias after meeting: damping in signal cable will slightly reduce the maximum amplitude). Check maximum input from ASIC.
- Pawel: ADC PCB are in production. Assembly starts soon.
- 2 for Mainz, 2 for Giessen (64 ASIC inputs)
- 1 for KVI: 16 linear inputs, 16 shaper inputs (optimized for Basel preamp)
- 1 for Uppsala
- Myroslav: Firmware for ADC to be ready in February.
- Matthias: External trigger input possible? Myroslav: Difficult, should put trigger on one channel and do by software. External trigger output: Difficult, large delay.
- Pawel: ADCs to be used in beam test beginning of March in Lund.
- Christoph: Define length of HV cables by end of Feb./March (ToDo: Claudius)
- Christoph: Example patch panel with SHV and Molex connectors shown. Check required size.
- Christoph: Should define length of patch cables from patch panel to ISEG HV in 2-3 weeks (1-2 m?)
- Myroslav: Rick is currently defining remaining info for interface pieces. The holes for mounting will be put on 2 sides. To be finished next week.
- Christoph: Plan for 50 spare inserts.
- Bochum: Wiener LV arrived. Has current offsets up to 200mA (Werner checked after meeting with Wiener: Precision is only 1% of 30A, is ok. Offset will be take in account in DCS. Action: Tobias)
- Christoph: 16x Alveoles ready, some need to be fixed by company. 8x Alveole production delayed (material availability)
- Bochum: APD and VPTT alveole dismounted. Pbs with gluing of some APDs. To be investigated.
- VPTT Alveole will be transported to Bonn for test setup
- Preamp 0.5V/pC output for VPTTs @12GeV, 1kV and 0.88T:
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
preamp_output.png | manage | 14 K | 2015-01-21 - 10:55 | FritzHerbertHeinsius | Preamp 0.5V/pC output for VPTTs @12GeV, 1kV and 0.88T |
Edit | Attach | Print version | History: r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r3 - 2015-01-23, FritzHerbertHeinsius
EMC Web
Web Home | Search Changes | Notifications Index | Topics
Web Home | Search Changes | Notifications Index | Topics
- Webs
- Cerenkov
- Cerenkov.Pandacerenkov
- DCS
- Daq
- Daq.Pandadaq
- Detector
- EMC
- EMPAnalysis
- Forwardstraws
- GEM
- MC
- Magnet
- Main
- Mvd
- PANDAMainz
- PWA
- Pbook
- Personalpages
- Physics
- Physics.Baryons
- Physics.CharmoniumAndExotics
- Physics.HadronsInNuclei
- Physics.OpenCharm
- PhysicsCmt
- SPC
- STT
- Sandbox
- ScrutinyGroup
- Tagpid
- Tagpid.Pandatagpid
- Tagtrk
- Tagtrk.Pandatagtrk
- Target
- Target.ClusterJetTarget
- Tof
- WebServices
- YoungScientists
- ZArchives
Create personal sidebar
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding Panda Wiki Send feedback | Imprint | Privacy Policy (in German)
Ideas, requests, problems regarding Panda Wiki Send feedback | Imprint | Privacy Policy (in German)


