You are here: Panda Wiki>Cerenkov Web>ResearchAndDevelopment>GeigerAPD (2007-06-20, BjoernSeitz)Edit Attach
Some information on SensL GeigerAPD
Please find three pictures sent by Deborah Herbert from SensL on this page. Here is the text I received from her.
"What makes this application challenging for the SPM is the very low light levels and additionally the fact that the interactions are not pulsed but a continuous stream of interactions (~2MHz rate) and there is no external trigger. Therefore the system needs to be self-triggering and be able to recognize an event itself. So considering that any one SPM unit will typically only see 1 photon and that the dark rate of the detector is at the level of 1 photoelectron, some other approach perhaps needs to be considered. One thing in our favour is that the Cherenkov light is emitted in a very short space of time (~ps) so all of the fired SPM elements will be fired simultaneously. Therefore, perhaps there is the possibility of some coincidence circuitry or summing in order to apply a discriminator, but there are a large number of channels involved
In order for you to have a better appreciation of the issues here, I have attached a few pictures to illustrate some of the key points. The first shows the output of a 1mm SPM in the dark. So the pulses you see are the noise (dark counts). These are due to thermally generated carriers in the active volume, and produce a pulse indistinguishable from a single photon interaction and are characterized by their rate. Typical rates for our SPMs are 1MHz/mm^2 which can be reduced by cooling and scales with area. The double pulse is due to cross-talk between microcells. It is an unwanted effect and will soon be omitted from our detectors by inclusion of technology to isolate the microcells from each other. The next picture shows the SPM illuminated with a low light level, fast pulsed LED. The display is the superposition of many events (persistence mode) to be able to see the different levels displayed by the differing numbers of photons detected in each pulse. Also visible are a couple of dark pulses. You see that they are the same amplitude as the single photon interactions from the LED and without a trigger (like I have here) you could not distinguish signal from noise. Like in your application, the photons are emitted in a brief space of time (5ns here), and so they stack up one on top of the other. So as soon as you have signals that give a signal >1 p.e. (assuming cross talk is omitted) then you can start discriminating between noise and signal. Just as an illustration, I have also included the charge histogram showing the peaks due to each of the levels shown on the scope.
I understand that your decision on the detector choice needs to be made by 2009 and the installation will occur in 2012.
As a way forward, I think it might be worthwhile for you to test one of our cooled 3mm SPMMinis to get a feel for its performance and use this to aid your thinking about the readout architecture and possible ways of discriminating your events. Whilst this is ongoing and if considered useful, we can consider issues such as the trade-off between using a green/red device to look at the 500nm+ wavelengths or the new blue/UV device to focus this narrower band."
-- BjoernSeitz - 20 Jun 2007
- first picture (cf text above):
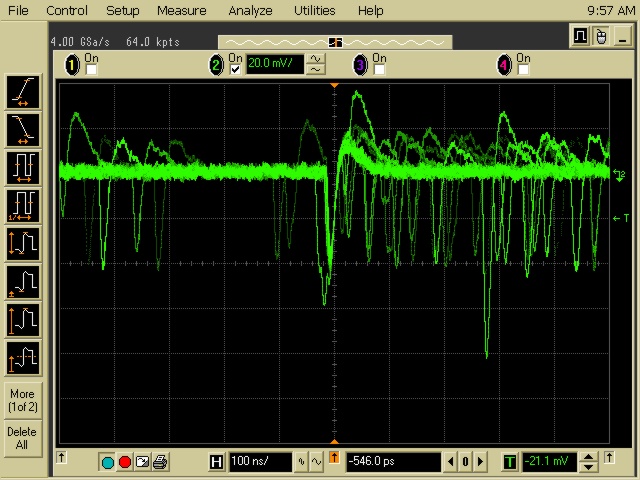
- second picture (cf text above):
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
070226_1mmlowlight_2amp_50Ohm.jpg | manage | 133 K | 2007-06-20 - 13:07 | BjoernSeitz | third picture (cf text above) |
| |
070302_darkcounts.jpg | manage | 124 K | 2007-06-20 - 13:05 | BjoernSeitz | first picture (cf text above) |
| |
SPS.JPG | manage | 25 K | 2007-06-20 - 13:06 | BjoernSeitz | second picture (cf text above) |
Edit | Attach | Print version | History: r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r1 - 2007-06-20, BjoernSeitz
Cerenkov Web
Web Home | Search Changes | Notifications Index | Topics
Web Home | Search Changes | Notifications Index | Topics
- Webs
- Cerenkov
- Cerenkov.Pandacerenkov
- DCS
- Daq
- Daq.Pandadaq
- Detector
- EMC
- EMPAnalysis
- Forwardstraws
- GEM
- MC
- Magnet
- Main
- Mvd
- PANDAMainz
- PWA
- Pbook
- Personalpages
- Physics
- Physics.Baryons
- Physics.CharmoniumAndExotics
- Physics.HadronsInNuclei
- Physics.OpenCharm
- PhysicsCmt
- SPC
- STT
- Sandbox
- ScrutinyGroup
- Tagpid
- Tagpid.Pandatagpid
- Tagtrk
- Tagtrk.Pandatagtrk
- Target
- Target.ClusterJetTarget
- Tof
- WebServices
- YoungScientists
- ZArchives
Create personal sidebar
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding Panda Wiki Send feedback | Imprint | Privacy Policy (in German)
Ideas, requests, problems regarding Panda Wiki Send feedback | Imprint | Privacy Policy (in German)


